![]() If you lookup group delay on Wikipedia, you'll find the following definition:
If you lookup group delay on Wikipedia, you'll find the following definition:
"Group delay is the time delay of the amplitude envelopes of the various sinusoidal components of a signal through a device under test (DUT)."
Where various can be thought of as assorted or mixed.
The first time I read that, my initial thought was: "Come again?". I mean seriously, what does that even mean?
During the past three years, this long-dreaded article has been slowly taking shape in my mind. Finally, I have found the courage to write it because frankly, I don't know if I even understand it myself. So here goes nothing.
Before we jump in at the deep end, let's start with phase delay first.
"Phase delay is the time delay of the phase experienced by the individual sinusoidal components."
To calculate phase delay in milliseconds use the following equation.
\begin{equation}\tau_{\phi}=-\left(\frac{\phi }{360}\times\frac{1000}{f}\right)\end{equation}
Where \(\phi\) is phase in degrees and \(f\) is frequency in hertz.
Notice the minus sign. I chose to ignore the minus sign for the better part of my career only to find out, the hard way, that it's there for a reason.
"Whether you owe me money or I owe you money,
the difference is only a minus sign."
Walter Lewin
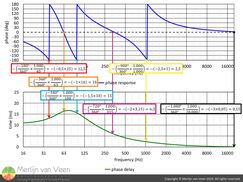 figure 1If we apply equation 1 to the phase response shown in figure 1, a typical response you would expect to see for a conventional 2-way loudspeaker, we obtain the green trace shown in the bottom chart of figure 1.
figure 1If we apply equation 1 to the phase response shown in figure 1, a typical response you would expect to see for a conventional 2-way loudspeaker, we obtain the green trace shown in the bottom chart of figure 1.
For this equation to work, it's mandatory to count phase, while being mindful of wraparounds, from low to high frequencies, or DC to daylight. Furthermore, as we're about to discover, do not automatically assume that 0° at 0 Hz implies no delay!
Undefined and indeterminate
To calculate phase angle from time delay in milliseconds use equation two.
\begin{equation}\phi=-\left(\frac{t}{T}\times360\right)=-\left(\frac{t}{\left[\frac{1000}{f}\right]}\times360\right)=-\left(t \times \frac{f}{1000}\times 360\right)\end{equation}
Where \(\phi\) is phase angle in degrees, \(t\) is time delay in milliseconds,
\(T\) is frequency time period in milliseconds, and \(f\) is frequency in hertz where \(f\neq0\).
Now to begin, DC or zero hertz isn't sinusoidal as in periodic and if you divide by zero bad things happen (so I'm told). The time period of zero hertz is undefined; there's no good definition for it. However, the one-sided limit for a frequency's time period \(\left(T=1000/f\right)\) in the denominator of equation 2, when frequency approaches DC from the right, explodes to infinity.
Therefore, if it takes you forever to finish a single cycle at DC, no amount of time delay will introduce a phase offset other than zero degrees which in the future might lead you to mistake zero degrees offset at DC for no time delay.
However, if you plug zero degrees at zero hertz into equation one, you get zero divided by zero, and even worse things will happen. This outcome is known as an indeterminate form which in this case means that the time delay cannot be determined. Any time delay at DC, will always result in a zero degree offset for reasons we discussed in the previous paragraphs.
If you use your loudspeaker management system to introduce 50 ms of delay into a delay loudspeaker feed, you're delaying all frequencies going to that loudspeaker including DC! It's just that zero hertz will always show up as zero degrees on a transfer function analyzer.
For more information about undefined expressions and indeterminate forms, please watch this excellent video by the Kahn Academy which helped me wrap my mind around it!
So please allow me to remind you and emphasize once more, for calculating phase delay make sure to count from low to high frequencies starting at 0 Hz! Now comes the caveat.
The caveat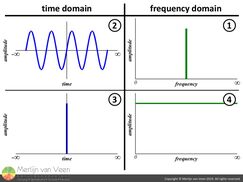 figure 2A perfect impulse in the frequency domain (figure 2.1), i.e., a single, infinitely narrow spectral line, requires a pure tone (sine wave) of infinite duration (figure 2.2), i.e., from Big Bang till the end of time.
figure 2A perfect impulse in the frequency domain (figure 2.1), i.e., a single, infinitely narrow spectral line, requires a pure tone (sine wave) of infinite duration (figure 2.2), i.e., from Big Bang till the end of time.
Conversely, a perfect impulse in the time domain (figure 2.3), i.e., an instantaneous rise and fall without over- or under-shoot, constitutes a spectrum with unlimited bandwidth (figure 2.4), i.e., from DC to the Planck frequency.
So what happens if we truncate our infinitely lasting sine wave to something more finite? Common sense suggests that its infinitely narrow spectral line should widen. By the time our sine wave lasts for only one sample, in other words a pulse, its bandwidth is unlimited.
Be sure to watch this wonderful video by 3Blue1Brown for a more in-depth explanation.
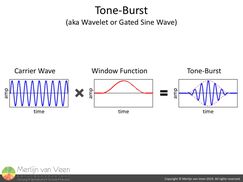 figure 3
figure 3
When you apply an amplitude envelope to a sine wave, modulating it's amplitude while truncating it in the process, you get what is known as a tone-burst, wavelet or gated sine wave (figure 3).
The latter being a tried-and-tested technique to beef up the sound of a kick drum (https://www.soundonsound.com/techniques/get-your-kicks).
"Why?" you might ask. Because a sine wave with an amplitude envelope applied to it, stops being a pure tone and becomes a group of frequencies which is where the group in group delay comes into play. From here on, I will refer to that sine wave as carrier wave.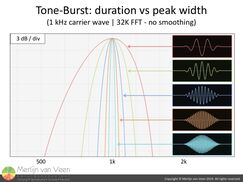 figure 4Figure 4 shows several amplitude-modulated carrier waves. In all instances, the carrier wave's frequency (1 kHz) is identical. The gate's attack, hold and release time together determine the amplitude envelope shape and duration.
figure 4Figure 4 shows several amplitude-modulated carrier waves. In all instances, the carrier wave's frequency (1 kHz) is identical. The gate's attack, hold and release time together determine the amplitude envelope shape and duration.
In this instance, a window function (Hann) was used to achieve the amplitude-modulating effect instead of an actual gate.
Notice that the width of the spectral peak which is no longer a pure tone but a now a group of frequencies, is inversely proportional to the duration of the tone bursts. Short bursts result in broad frequency groups whereas long bursts result in narrow frequency groups. Ultimately, an infinitely long burst (carrier wave without envelope - figure 2.2) would produce an infinitely thin spectral line (figure 2.1).
Please watch the video below to hear this in action (use headphones or full range loudspeakers - audio right channel only).
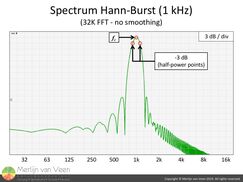 figure 5The Hann tone-burst or Hann-burst (Don Keele) shown in figure 3 has a bandwidth of one-third octave between the -3 dB (half power) points (figure 5).
figure 5The Hann tone-burst or Hann-burst (Don Keele) shown in figure 3 has a bandwidth of one-third octave between the -3 dB (half power) points (figure 5).
There's a tone burst for each third-octave frequency which you can download here. It's a reasonably dynamic (test) signal where one burst has a crest factor of 7,3 dB.
These bursts are also used for measuring distortion in subwoofers according to the ANSI/CEA-2010 standard.
Delay of the amplitude envelope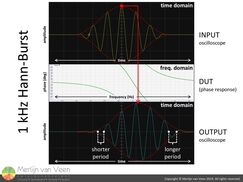 figure 6Now that we have an actual group of frequencies, represented by an amplitude‑modulated carrier wave, we can use an oscilloscope to observe the delay of the amplitude envelope's crest or crescendo by a DUT that introduces a gratuitous amount of phase shift.
figure 6Now that we have an actual group of frequencies, represented by an amplitude‑modulated carrier wave, we can use an oscilloscope to observe the delay of the amplitude envelope's crest or crescendo by a DUT that introduces a gratuitous amount of phase shift.
Figure 6 shows a group of frequencies, centered at 1 kHz, being transferred through a DUT that exhibits -360° of phase shift (relative to 0° at 0 Hz) at 1 kHz.
Notice the stretching of the imaginary amplitude envelope. Its crest shifting to the right (indicated by the red arrow). The amplitude envelope's crescendo for the one-third-octave-wide group of frequencies has been time delayed.
The group of frequencies is decomposed and its component frequencies' phases have been delayed (phase delay).
For negative phase slopes (middle plot in figure 6) whose slope is not constant (on a linear scale) over frequency, the component frequencies' phase delay is not identical (dispersion), making higher frequencies (shorter period) "group-leaders" and lower frequencies (longer period) "group-trailers". Contrary to the original input signal, whose carrier wave's time period remained constant, the output signal's carrier wave has become somewhat of a swept sine wave whose time period changes over time.
The DUT's continuously changing phase shift, throughout the group's one-third-octave-wide frequency span, has rearranged its constituent sinusoidal components in a way which postpones the group's crescendo and delays the amplitude envelope.
The train station
To repeat the process for the entire audible range, you can resort to a wavelet transform which shows you only the amplitude envelopes without the carrier waves "underneath" on a spectrograph.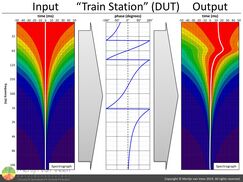 figure 7If you put twenty thousand (the entire audible band) of those amplitude envelopes into a DUT at once, and observe the outcome on a spectrogram, it's apparent that the DUT delays the amplitude envelopes' crests (figure 7).
figure 7If you put twenty thousand (the entire audible band) of those amplitude envelopes into a DUT at once, and observe the outcome on a spectrogram, it's apparent that the DUT delays the amplitude envelopes' crests (figure 7).
The continuous white line, that connects the adjacent amplitude envelopes' crests, represents the group delay and is a function of frequency. Modern analyzers will display group delay without having to resort to wavelet transforms, and the resulting time‑over‑frequency plot will be identical to the continuous white line shown in the output spectrograph of figure 7.
I call it the train-station-effect where you have cars, containing groups of frequencies, going into the station all at once which come out of the other end of the station in a different order. Some cars have fallen behind, they linger and are sustained.
In the video below (use headphones or full range loudspeakers), I send a red pulse (pulse with a red spectrum [-3 dB/oct] ) through a DUT which exhibits a lot of phase shift at 100 Hz.
I start with a null-test which is suited for exposing the residual difference between a processed and unprocessed version of the same signal.
Notice that the processed version, with the phase shift, sounds sustained. There's audible pitch which decays over time like a damped resonance or ringing. The 100 Hz car and its passengers (sinusoidal components) are late to the party. The remaining cars came out of the train station simultaneously.
Which brings us to my favorite definition of group delay:
"The subjective effect of excessive group delay is a “loosening” of the bass or a “less dry” bass quality."
Neumann
If you ever have the opportunity to listen to the Meyer Sound Bluehorn System where virtually all phase shift, and inherently group delay, has been removed, you'll understand why this quote resonates with me.
The distinction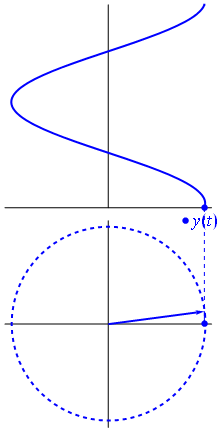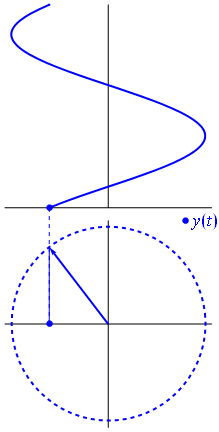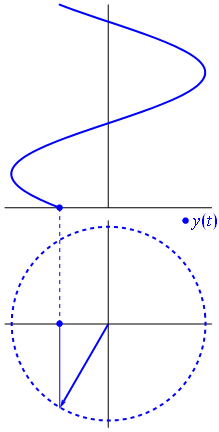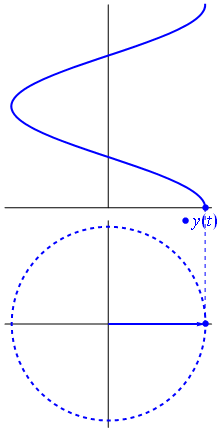 figure 8Phase delay, discussed at the beginning of this article, represents the time delay of the carrier waves' phase.
figure 8Phase delay, discussed at the beginning of this article, represents the time delay of the carrier waves' phase.
The carrier waves can be represented by phasors (a portmanteau of phase vector) where amplitude and phase are easy to distinguish from each other (figure 8).
The phase portion solely determines the initial condition, like the hand of a clock, when you hit "play".
A sine wave with ninety degrees offset, starts off as a cosine wave when you hit "play". Regardless, with or without phase offset, in either case, when your press "play", there will be sound.
Can you hear the difference between a sine wave generator and a cosine wave generator?
Contrary, for finite carrier waves which translate into groups of frequencies, group delay indicates the arrival time of the bulk (center of mass or crescendo) of energy over frequency which shouldn't be mistaken for signal arrival time.
In case of beefing up the kick drum, the oscillator is running for the duration of the entire show, but there's only audible sound when the kick drum microphone triggers the gate inserted into the oscillator's channel.
Does that mean that the oscillator's sine wave signal has arrived now that we can finally hear it? That is was "in transit" all the time while the gate was closed?
Phase formula
You can calculate and approximate group delay in milliseconds by applying the phase formula.
\begin{equation}\tau_{g}=-\left(\frac{\frac{\left[\phi_{hi}-\phi_{lo}\right]}{360}}{\left[f_{hi}-f_{lo}\right]}\times 1000 \right)\end{equation}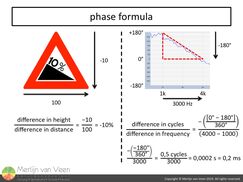 figure 9
figure 9 figure 10
figure 10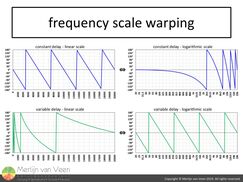 figure 11Equation 3 calculates the slope of a secant line connecting two points on a phase trace (figure 9).
figure 11Equation 3 calculates the slope of a secant line connecting two points on a phase trace (figure 9).
Similar to phase delay, the unit is indeed time (figure 10) which shouldn't be mistaken for signal arrival time! Just like baby oil isn't made of babies contrary to olive oil.
The phase formula is prone to error because what appear to be straight lines on a logarithmic scale are in actuality curved lines when observed on a linear scale. A phenomenon which I've come to call frequency-scale-warping (figure 11).
So, depending on the interval (frequency span) you choose, your secant line is likely to be a crude approximation. Only when you make your interval infinitely small (limiting case) does the secant line become the tangent line to the phase trace which is ultimately what we're after.
That's why I'm strongly opposed to using the phase formula for time aligning main speakers to subwoofers which only works if:
- Both loudspeakers are phase compliant
(matched phase responses throughout the crossover range) - You choose the same interval (frequency span) for both phase traces
What I've been teaching for the past years is, using equation 1 which allows you to convert a phase offset into a time offset, to achieve phase alignment for a single frequency in the crossover range first which always works.
Once you've succeeded at that, you should evaluate your slopes throughout the crossover range and determine if they match. Do they exhibit the same slope, regardless of how the slopes themselves look!
It the slopes don't match, it means that your not in the same cycle (or close to), which can be addressed by adding \(n\) cycles or \(\left(n+0,5\right)\) cycles of delay in combination with a polarity reversal (where \(n\) can be zero, i.e., half a cycle) of delay, for that single frequency you previously phase aligned, to the shallowest slope.
And last but not least, set your delay finder only once!
A complete and foolproof method for phase aligning mains to subs can be found here.
To understand the importance of matched slopes be sure to watch this video.
When is group delay equal to phase delay?
Group delay is the first derivative of phase delay, so in order to answer this question you need to solve the differential equation \(\tau_{g}(f)=\tau_{\phi}(f)\) which solution is any constant (function).
Long story short, only when you're dealing with a constant time delay (constant phase slope on a linear scale) for all frequencies (including a microphone cable with no delay) are phase and group delay the same.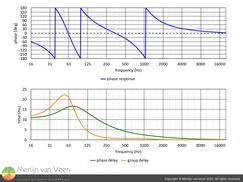 figure 12
figure 12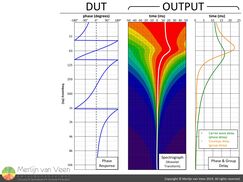 Figure 13However, when time delay changes with frequency (like real loudspeakers) phase delay and group delay start to diverge (figure 12).
Figure 13However, when time delay changes with frequency (like real loudspeakers) phase delay and group delay start to diverge (figure 12).
Notice however, that when the rate of change in the phase response is very little, to the point of almost become a constant slope (at very low and high frequencies), phase and group delay converge.
Figure 13 shows all the relevant charts together. Notice that the wavelet transform from figure 7 is in perfect agreement (as promised) with the calculated derivative of the DUT's phase response.
Phase Delay in Action
Please watch the video below to see phase delay in action.
