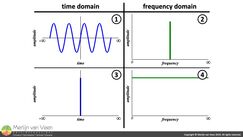
Figure 1What constitutes a group of frequencies and how does that relate to the word "group" in group delay.

Most audio professionals feel pretty comfortable with the reciprocal relationship between time and frequency.

\begin{equation}T=\frac{1}{f}\end{equation}
Where \(f\) is frequency in hertz and \(T\) is time period in seconds.

Subsequently, high frequencies have short time periods whereas low frequencies have long time periods. However, this familiar reciprocal relationship feels less intuitive when applied to observations made in the time and frequency domains.

A pure tone (without harmonics) that lasts forever (Figure 1.1) appears as a single — infinitely narrow — spectral line in a frequency spectrum (Figure 1.2).

Therefore — by reciprocity — a perfect impulse on an oscilloscope (Figure 1.3), i.e., an instantaneous rise and fall without over- or under‑shoot, consists of infinitely many frequencies (Figure 1.4). To paraphrase Richard C. Heyser:

"A perfect impulse in the frequency domain represents one — everlasting — frequency. A perfect — infinitely short — impulse in the time domain represents all frequencies."

Notice the reciprocity: everlasting versus infinitely short. Why is that and what happens in between these extremes?

Constructing a Pulse

Let us construct a pulse by adding a bunch of — phase‑aligned — pure tones.

Figure 2In Figure 2.1 we start with the line spectrum (no banding) of a single pure tone at 1 kHz. In order for this spectral line to be infinitely narrow so that it describes the energy exclusively at 1 kHz — without uncertainty — and no other, adjacent frequencies, the pure tone would have to last forever (Figure 2.3).

So what happens when we increase the bandwidth of our pure tone by adding — phases aligned — all neighboring frequencies that live within an 1‑octave‑wide interval centered at 1 kHz?

Figure 2.4 shows the perfect 1‑octave‑wide — brick wall — pass‑band centered at 1 kHz. Figure 2.5 shows the individual oscillograms for a subset (not to be mistaken for a Fourier series) of the — infinitely many and everlasting — sinusoidal components, i.e., pure tones, that live within that single octave. Notice, by looking at \(t=0\), that their phases are aligned whereas to the left and right there is "coordinated phase chaos."

If we add the infinitely many sinusoidal components that live within this single octave together — not just the subset shown in Figure 2.5 — we get the combined waveform shown in Figure 2.6. Notice that where there is "coordinated phase chaos" in the plot directly above (Figure 2.5), the combined amplitude — when summed together — regresses to zero. Only the region around \(t=0\) shows substantial oscillation. Essentially, we now have a 1‑kHz carrier wave with an amplitude envelope applied to it.

The "coordinated phase chaos" among the individual sinusoidal components (apart from around \(t=0\) ) — in concert — has "amplitude‑tapered" the beginning and ending of the 1 kHz pure tone we began with. The everlasting 1 kHz pure tone shown in Figure 2.3 (to the left of Figure 2.6) has effectively become — truncated — in the process. Its duration shortened from infinity to a couple of milliseconds.

Subsequently, the remaining waveform in Figure 2.6 is no longer a pure tone, but rather an octave‑wide — group — of frequencies (Figure 2.4). A burst or an "imperfect" pulse.

Bandwidth-Duration Relationship

The duration of the pulse or burst shown in Figure 2.6 is inversely proportional to the bandwidth of the "group" of frequencies. When bandwidth is increased (Figure 2.7) the group gains more "members" whose "coordinated phase chaos" (Figure 2.8) — apart from around \(t=0\) — exacerbates the amplitude tapering of the carrier wave. Notice in Figure 2.9 that the amplitude envelope got "pinched" when bandwidth was increased. The pulse is now much short than before (Figure 2.6 to the left of Figure 2.9).

When this is taken to the extreme, by increasing the bandwidth so that — all possible frequencies (including inaudible ones) — are included, the amplitude envelope will get pinched or squeezed even further and approach a perfect — infinitely narrow — (im)pulse which inherently represents all frequencies. Hence, Figure 1.

We went from an everlasting narrowband signal without envelope to a finite broadband signal with infinitely short envelope.

As far as the author knows, it is impossible to create a perfect brick‑wall band‑pass filter as shown in Figure 2.4, so let us look at a slightly different example.

Gated Sine Wave

Figure 3Figure 4Figure 3 shows a similar exercise where the amplitude at the pass‑band edges rolls off rather than being a brick‑wall transition. Nevertheless — once the carrier wave has been truncated — the result is no longer a pure tone but rather a group of frequencies whose bandwidth is inversely proportional to the duration of the remaining pulse.

Unlike the brick‑wall example in Figure 2, such a band‑passed signal is very easy to create and is used more often than you may realize.

Notice that the waveform in Figure 3.6 resembles the "gated sine wave" shown in Figure 4. A tried‑and‑tested technique to beef up the sound of a kick drum where a tone generator runs through a compressor whose gate is triggered by the kick drum microphone (https://www.soundonsound.com/techniques/get-your-kicks).

By now, you should be able to appreciate that the pitch of this sound will be determined by the tone generator's frequency (carrier wave) whereas the bandwidth of the sound will be determined by how long the gate is open (amplitude envelope). The result does not sound like a tone but rather like a "thud" with pitch.

Conclusion

Besides harmonics, practical signals of finite duration, e.g., a drum hit, a keystroke, a plucked note, or a spoken syllable, all may have pitch but invariably consist of more than one frequency. They are inherently groups of frequencies. Subsequently, the word group in "group delay", by definition, implies that the delay — never — applies to single discrete frequency. More soon!

In the mean time, for more information about group delay, please read Group Delay 101.




This article is also featured in the May 2022 issue of Live Sound International magazine.