What does it take to achieve good cancellation? In order to explain this, I like to use a concept that I refer to as "The Center of Tranquility at the Eye of the Storm".
For two signals to cancel each other—they have to be correlated—i.e., their waveforms (as seen on an oscilloscope) have to match (same shape) and be in phase opposition. Uncorrelated signals are immune to time offsets as well as polarity reversals.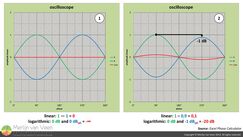
Figure 1Example 1 in Figure 1 shows two sine waves (pure tones) whose amplitudes are matched, but where one instance (B) has been polarity reversed.
Reversing the polarity of one signal—flips its sign—and effectively turns addition into subtraction upon combination. When we subtract these two parts from each other the remainder is zero, where zero—on a linear scale—maps to minus infinity in decibels on a logarithmic scale.
Example 2 in Figure 1 shows the same sine waves as before where instance (B)—in addition to the polarity reversal—now also is attenuated by 1 dB. After subtraction, the remainder is no longer zero and cancellation went from minus infinity to -20 dB. That single dB offset made an infinite difference in cancellation!
So what happens when we are no longer in perfect phase opposition, like with the polarity reversal, while levels continue to remain matched?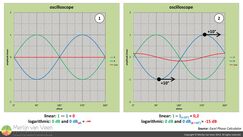
Figure 2Example 2 in Figure 2 shows the same sine waves where instance (B)—in addition to the polarity reversal—has been shifted to the right by 10°. Again, the remainder is no longer zero and cancellation went from minus infinity to -15 dB. That mere 10° offset made an infinite difference in cancellation!
So far, we can conclude that, in order to achieve perfect cancellation, i.e., minus infinity (in dB), signals need to be correlated, perfectly level matched, and in perfect phase opposition (reversed).
It is rare for any pair of brand new loudspeakers (or systems), of the same make and model, to be perfectly level-matched out of the box, or remain matched over time. After all, e.g., a 10% tolerance in a resistor equals one dB, and that is just one example of the many parts used in loudspeaker systems. Products with a level potentiometer are even more prone to subtle level differences.
Enter the Storm
I have yet to experience perfect cancellation in the field, using vanilla loudspeakers, and wonder if it can be done. So what if we lower our expectations, and aim for something more moderate such as 15 dB of cancellation.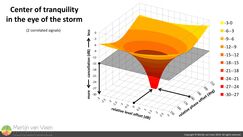 
Figure 3Figure 3 shows the "funnel" which kinda resembles a tornado. Purportedly, at the center of a tornado, in the eye of the storm, there's tranquility, i.e., clear blue sky and sun shining. At the base of the funnel in Figure 3, there is also "tranquility" in the form of silence.
In order to end up at the base of the funnel—where maximum cancellation occurs—levels need to be perfectly matched and in perfect phase opposition (reversed). Once either condition is no longer met, you go up the funnel (along its walls), where cancellation is less and things get louder.
If we bisect the funnel (roughly) in half at -15 dB of cancellation, the challenge becomes to end up in the bottom part of the funnel, below the bisecting (grey) plane.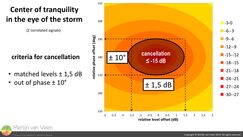
Figure 4Figure 4 lets us observe the very same funnel directly from above. Notice the dark oval shape where the grey plane bisects the funnel. This is our destination, and in order to get there, we can derive the following (stringent) conditions:
- matched levels ± 1,5 dB or less
- out of phase ± 10° or less
When either condition is not met, you go up the funnel (along its walls), where cancellation is less and things get louder.
One dB is the Just Noticeable Level (JND) or smallest audible step for sound levels, and ten degrees at, e.g., 100 Hz, equals (10° / 360°) x 10 ms = 0,3 ms. Suffices to say, these rules‑of‑engagement are quite stringent, even at lower frequencies...
15 dB is a shedload
Figure 5Fifteen dB of cancellation might sound like very little, but the Equal Loudness Contours (Figure 5)—which admittedly only apply to pure tones—suggest that our hearing sense is more sensitive to relative pressure differences at low frequencies.
It takes a 10 dB increase in SPL—for frequencies above 1 kHz—to achieve a 10 phon increase (subjective doubling) in perceived loudness, whereas at low frequencies, only 5 dB is needed to achieve the same 10 phon increase.
Therefore, 15 dB less SPL—at low frequencies—is 30 phon less loud and 23 = 8 times quieter subjectively!
The first time I became aware of this behavior, was when I visited the late Siegfried Linkwitz's website many years ago. Click here to read his article that covers this.
Realistic goals
When I am asked to design solutions that cancel by committee (typically subwoofer arrays), I aim for at least 15 dB of cancellation. If, on site, it turns out to be more, I consider it a good day. Anything less, requires me to go back to the drafting table.
Fifteen dB of cancellation is doable, and frankly as good as it typically gets. More often than not—there is neither the time nor the resources—to tweak every single element in a system by: fractions of a decibel, fractions of a millisecond, or fractions of an inch to compensate for inevitable deviations in the field.
The images in this article were made with the phase calculator which you can download for free at the link shown below:
https://www.merlijnvanveen.nl/en/calculators/46-phase
This article is also featured in the June 2021 issue of Live Sound International magazine.