 Why a specification like "We need a sound system capable of delivering full range 103 dB(A) of clear and undistorted sound at the front of house position" makes me scratch my head.
Why a specification like "We need a sound system capable of delivering full range 103 dB(A) of clear and undistorted sound at the front of house position" makes me scratch my head.
Because, typically the mix doesn't exhibit an A-weighted spectrum.
Even as a precautionary measure to make sure the sound system is capable of handling the show, this remains a questionable specification. Never mind that it doesn't mention an integration time (average) e.g. 1 second, 5 minutes or 2 hours or how long that desired level should be maintained? What makes specifications like these questionable, is the full range A-weighting specification.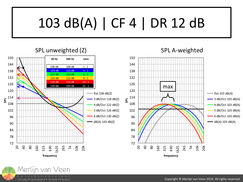 figure 1
figure 1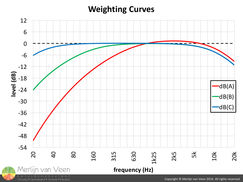 figure 2Figure 1 shows various spectra (absolute SPL) in an unweighted (Zero) and weighted (A) fashion. All these spectra read 103 dB(A) with pink noise on a sound level meter using A-weighting. The weighting curves (figure 2) are derived from the Fletcher-Munson curves which predate WWII. Specifically at lower frequencies our ears are less sensitive to pressure.
figure 2Figure 1 shows various spectra (absolute SPL) in an unweighted (Zero) and weighted (A) fashion. All these spectra read 103 dB(A) with pink noise on a sound level meter using A-weighting. The weighting curves (figure 2) are derived from the Fletcher-Munson curves which predate WWII. Specifically at lower frequencies our ears are less sensitive to pressure.
A-weighting is used to mimic our ear's non-linear loudness perception over frequency at low levels. According to today's Equal Loudness Contours it represents 60 phon i.e. conversational speech or background music which is quite peculiar given the levels of concerts. The B-weighting in contrast, represents the ear's behavior at high SPL (100-110 phon).
The black line in the right hand chart of figure 1, shows a flat A-weighted spectrum of 103 dB. If we look at the unweighted or Z-weighted values in the left hand chart of figure 1, we can see this would require 140 dB of SPL at 40 Hz. So how many subwoofers would it require to deliver that much pressure at FOH?
When we move towards FOH, we lose 6 dB of pressure for each doubling in distance (inverse square law) and the only way to counter this (delay subs excluded) is by increasing the number of subwoofers. figure 3Figure 3 shows 6 different models of dual 18" subwoofers by 6 different manufacturers, producing continuous pink noise under half space (ground stacking) conditions, with a crest factor of 4 : 1 or a dynamic range of 12 dB if you will.
figure 3Figure 3 shows 6 different models of dual 18" subwoofers by 6 different manufacturers, producing continuous pink noise under half space (ground stacking) conditions, with a crest factor of 4 : 1 or a dynamic range of 12 dB if you will.
Imagine a pile of subwoofers on the floor, spaced closely together in an attempt to achieve maximum coupling and therefor efficiency which in practice won't succeed because their physical size prevents this.
Notice in figure 3 how most manufacturers would require 24 to 32 subwoofers to produce levels around 140 dB (103 dB(A) @ 40 Hz) at merely 8 meters (26 ft). That's a lot of subwoofers and we haven't even left the penalty area of a soccer pitch!
DISCLAIMER: These tables are based directly on manufacturer published specification sheets. Please handle them with caution. The criteria that constitute peak output and how gracious the speakers go about it, are unknown.
Even with really long (line) arrays of subwoofers, the cylindrical waves that drop at only 3 dB per doubling distance would have limited merit as is shown in the bottom left table of figure 3. This table shows the line length (no. of speakers times spacing) required to extent the cylindrical wave behavior up to a certain distance, until it falls back to spherical wave behavior with 6 dB per doubling distance (inverse square law).
The sheer number of subwoofers required to achieve full range 103 dB(A) of sound pressure, is what makes the A-weighted specification questionable which raises the question if we need that much pressure?
Personal observations suggest a trend in the spectral composition of typical contemporary live sound mixes. Most mixes appear to show an gentle continuous declining slope from low to high frequencies in order of 3 to 6 dB per octave (left hand chart in figure 1). That's 27 (9 x 3) to 54 (9 x 6) dB of tonal change respectively, in the 9 octaves between 32 Hz and 16 kHz.
A glance at the A-weighted values in the right hand chart of figure 1 shows that, depending on the slope, these tonal trends will peak out first in the octaves between 250 Hz and 1 kHz. These are typically the first frequencies that reach the SPL limit, if applicable. Not the low end.
The left hand chart reveals that at 40 Hz, 134 dB of unweighted pressure for the steepest slope (most sub heavy mix) will do, in contrast to the overestimated value of 140 dB for 103 dB(A) full range. That's 50% less subwoofers!
The tables in figure 3 inform us that we therfor could cover twice the distance (16 meters 52 ft) with the same amount of subwoofers required for the 103 dB(A) full range SPL at merely 8 meters (52 ft)!
The gentlest slope (least sub heavy mix) could cover even 64 meters (210 ft) using the same amount of subwoofers to achieve 123 dB of unweighted pressure for 40 Hz at 64 meters (210 ft).
So depending on the application, typically between 10 and 32 subwoofers in half-space, with music exhibiting a dynamic range of 12 dB or less, goes a long way. If you would like to build in some headroom, scale the number of subwoofers accordingly. 140% for 3 dB and 200% for 6 dB. Unfortunately in practice sound systems tend to go as loud as we can afford...
Coverage control in general, by means of cardioid configurations and/or arrays comes at a price which is typically a reduction in SPL and should be compensated accordingly. The End-Fire array is an exception.
So ultimately, the number of subwoofers required depends on:
- the unweighted spectrum of the program material and how this translates to the weighted sound level meter
- the dynamic range of the program material
- the distance that needs to be crossed
- coverage control
- headroom
But hardly ever is an amount of subwoofers, required to achieve values of 103 dB(A) at 40 Hz (140 dB SPL at 1 m [3 ft.]), called for.
Watch the video by Meyer Sound below to see how program material affects maximum SPL.
Real World SPL from Meyer Sound on Vimeo.
